DISTILL (LRI)
DISTILL aims at mapping the problem domain onto a metric space, because a
number of robust data analysis algorithms are applicable into
metric spaces, to various aims (discrimination, regression, clustering,
visualization,...).
One first remarks that a set of disjunctive hypotheses
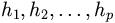 defines a mapping from the problem
domain
defines a mapping from the problem
domain  onto the space of integer
vectors
onto the space of integer
vectors  .
Let h be given as
.
Let h be given as  , where
, where
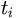 are conjunctive hypotheses in
are conjunctive hypotheses in
 . Let <E,h> denote the
number of
. Let <E,h> denote the
number of 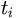 which subsume E.
The mapping
which subsume E.
The mapping 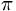 from the problem
domain
from the problem
domain  onto
onto
 is defined as follows:
is defined as follows:

By the way, this mapping onto the metric space  automatically defines a metric structure on
automatically defines a metric structure on  :
:
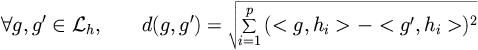
Expectedly, the relevance of this metric structure increases with the
number p of hypotheses hi considered, and the diversity of these
hypotheses. This relevance will be empirically estimated from the
predictive accuracy of a k-nearest neighbor classification process based on
the above distance.
Hypotheses 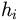 are termed dimensions of
the mapping
are termed dimensions of
the mapping 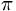 , and p is the
user-supplied number of dimensions. DISTILL uses fragments of hypotheses
built by STILL (see) as dimensions of
, and p is the
user-supplied number of dimensions. DISTILL uses fragments of hypotheses
built by STILL (see) as dimensions of  :
p pairs of examples (
:
p pairs of examples ( ,
,
 ) are randomly selected; hypothesis
) are randomly selected; hypothesis
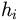 is set to the disjunctive hypothesis
D(
is set to the disjunctive hypothesis
D( ,
,  ),
which covers
),
which covers  and discriminates
and discriminates
 . Thanks to the stochastic subsumption
mechanism of STILL,
. Thanks to the stochastic subsumption
mechanism of STILL, 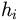 can be approximately
characterized and used with linear complexity in the size of the examples.
DISTILL complexity (computing the distance of any two examples) finally is
can be approximately
characterized and used with linear complexity in the size of the examples.
DISTILL complexity (computing the distance of any two examples) finally is
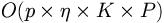
where p is the number of dimensions,  the number of samples considered during induction, K the number of
samples considered during classification, and p the maximum number of
literals of an example.
the number of samples considered during induction, K the number of
samples considered during classification, and p the maximum number of
literals of an example.
DISTILL involves one parameter less-than STILL: parameters
 and M,
which control the consistency and generality requirements in STILL, are
replaced by the number of dimensions p.
and M,
which control the consistency and generality requirements in STILL, are
replaced by the number of dimensions p.
back to index
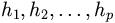 defines a mapping from the problem
domain
defines a mapping from the problem
domain  onto the space of integer
vectors
onto the space of integer
vectors  .
Let h be given as
.
Let h be given as  , where
, where
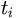 are conjunctive hypotheses in
are conjunctive hypotheses in
 . Let <E,h> denote the
number of
. Let <E,h> denote the
number of 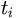 which subsume E.
The mapping
which subsume E.
The mapping 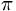 from the problem
domain
from the problem
domain  onto
onto
 is defined as follows:
is defined as follows:

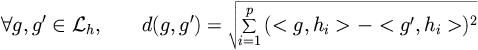
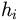 are termed dimensions of
the mapping
are termed dimensions of
the mapping  ,
,
 ) are randomly selected; hypothesis
) are randomly selected; hypothesis
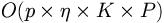
 the number of samples considered during induction, K the number of
samples considered during classification, and p the maximum number of
literals of an example.
the number of samples considered during induction, K the number of
samples considered during classification, and p the maximum number of
literals of an example.
 and M,
which control the consistency and generality requirements in STILL, are
replaced by the number of dimensions p.
and M,
which control the consistency and generality requirements in STILL, are
replaced by the number of dimensions p.