Steel Grinding (LAI)
The task in the steel grinding domain is to determine the
roughness of the workpiece from the properties of the sound produced during
the process of steel grinding. The broader aim of the study was to elaborate
the results from the point of view of machine control, where the task is
to perform relevant control actions in response to parameter values monitored
during the process execution. Since control action is easily deducible
from workpiece roughness, the subproblem of workpiece roughness estimation
was addressed first. Several machine learning techniques were already applied
to the problem, yielding encouraging results (Filipic et al. 1991).
| Application domain: |
Steel Grinding |
| Further specification: |
Data set |
| Pointers: |
Contact Aram Karalic Aram.Karalic@ijs.si |
| Data complexity: |
123 examples |
| Data format: |
Prolog |
FORS Experiments
Data were obtained during an experiment in which vibration
signals generated by the grinding wheel and the workpiece were detected
by an accelerometer sensor and processed by a spectrum analyzer (Junkar
et al. 1991). From the obtained spectra predefined spectral features were
extracted: total spectrum area (SpArea), frequency of
the maximum area peak (MaxAreaX), and frequency of the
spectrum area central point (AreaCX). Simultaneously, workpiece
surface roughness was measured.
Two background knowledge literals were defined: =<
and >=, enabling FORS to compare the frequencies.
Expert's Evaluation and Conclusions
It turned out that the use of background knowledge did not
bring any significant improvement in the model quality in terms of RE.
However, the newly induced models frequently contained background knowledge
literals. The domain experts considered this a significant improvement
because newly induced models are more general than the models without
background knowledge. For example, without using background knowledge,
a literal such as MaxAreaX <= 6125 typically appeared, saying
that the frequency of the maximum area peak is less than 6125Hz. In this
particular setting (grinding regime, choice of the tools) this means that
the maximum area peak is in the lower part of the spectrum. Using different
grinding wheel speed the whole spectrum would shift to higher or lower
frequencies, thus making the above literal useless. However, usage of background
knowledge typically yielded literal MaxAreaX <= AreaCX, which
directly states that the maximum peak must lie in the lower part of the
spectrum, regardless of the frequency area in which the spectrum is situated,
therefore enabling rule usage in much broader class of working regimes.
The model using linear regression constructed from all
examples by using MDL pruning was chosen for closer inspection:
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
AreaCX =< 5600, MaxAreaX <= AreaCX,
SpArea =< 0.25, Roughness is 1.70,!.
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
MaxAreaX <= AreaCX, AreaCX =< 5890,
MaxAreaX =< 1140,
Roughness is 0.00169 * MaxAreaX,!.
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
AreaCX >= 7310, SpArea >= 0.2130,
Roughness is 0.00016832 * AreaCX,!.
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
MaxAreaX <= AreaCX, SpArea >= 0.33,
AreaCX >= 5950,
Roughness is 0.00029 * AreaCX,!.
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
SpArea =< 0.1700, Roughness is 0.98,!.
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
AreaCX =< 5890, Roughness is 1.72,!.
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
SpArea =< 0.23,
Roughness is 5.4102 * SpArea,!.
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
SpArea >= 0.31, AreaCX >= 6190,
Roughness is 1.38,!.
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
MaxAreaX >= 5730, SpArea >= 0.33,
Roughness is 4.13661194 * SpArea,!.
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
AreaCX <= MaxAreaX, Roughness is 1.28,!.
f(Roughness,SpArea,MaxAreaX,AreaCX) :-
Roughness is 1.82,!.
Expert's evaluation of the model follows:
-
The condition of the first clause has three parts. The
first part selects low frequency of the spectrum central point, that is,
small average number of cutting particles. At a simultaneous requirement
for a frequency of the central point to be larger than the frequency of
the maximum peak it also confines the frequency of the maximum peak to
be at least 1140Hz. This yields rather large roughness which means that
low frequencies of the maximum area peak imply large roughness. This indicates
that roughness is determined by the largest particles, since even relatively
small number of such particles can easy spoil the surface.
-
Second clause confines the frequency of the area central
point to the narrow interval between 5600Hz and 5890Hz and with the other
part of the condition equal to the first condition, estimates roughness
as a linear function of the maximum peak frequency. The clause excellently
describes a group of data points near the largest frequency 1100Hz (Figure
1). This clause is also consistent with the first two models, except that
the roughness is this time described as a function.
-
Clause number 3 tells us that high frequency of the area
central point and small spectrum area imply low roughness. The following
rule is clearly revealed: a large average number of cutting particles (small
particles) and low spectrum area imply low roughness.
-
Clause 4 describes a group of measurements with low highest
frequencies of the spectrum. In spite of high frequency of the spectrum
area central point (one would then expect small roughness), we get, at
the simultaneous high spectrum area (
 the power), a large roughness. The roughness in this situation linearly
increases with the frequency of the area central point. This clause again
states that a small number of large particles can significantly spoil the
surface.
the power), a large roughness. The roughness in this situation linearly
increases with the frequency of the area central point. This clause again
states that a small number of large particles can significantly spoil the
surface.
-
Clause five tells us that the roughness is low when the
power of the process is low, independently of the size of the particles.
-
Clause six again confirms the fact that the largest particles
determine the quality of the surface. Small average number of cutting particles
implies bad surface.
-
Clauses 7, 8, and 9 split the parameter space according
to the spectrum area and assign each subspace a linear relationship between
the roughness and the spectrum area, thus confirming the fact that larger
cutting power implies bad surface.
0.8mm
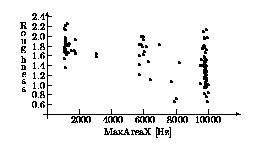
Figure 1: Roughness vs. frequency of the maximum
area peak (MaxAreaX) in the domain of steel grinding. Domain expert
claims to be satisfied with the results of machine learning since our models
enabled him to grasp some additional process properties which he wouldn't
be able to discover only with classical statistical tools. However, he
suggests that the machine learning approach should not be used alone but
should be considered as a powerful supplement to the already existent instruments.
It is also worth noting that if the expert had to choose between two equally
good models in terms of RE, he usually chose the larger model, justifying
the decision by stating that the smaller model does not grasp sufficient
detail. However, when choosing amongst the models which had 1, 2 or 3 variables
in linear regression terms, he chose the model with only one variable in
linear regression terms claiming that it is easier to understand. He also
preferred such models over the models with no linear regression.
References
-
Bogdan Filipic, Miha Junkar, Ivan Bratko, and Aram Karalic.
An application of machine learning to a metal-working process. In Proceedings
of ITI-91, pages 167-172, Cavtat, Croatia, 1991.
-
Miha Junkar, Bogdan Filipic, and Ivan Bratko. Identifying
the grinding process by means of inductive machine learning. In Preprints
of the first CIRP Workshop on Intelligent Manufacturing Systems, Budapest,
Hungary, 1991.
-
A. Karalic, I. Komel, R. Posel. Applications of artificial
intelligence in mechanical engineering. In B. Zajc, F. Solina (eds.) Proceedings
of the Fifth Electrotechnical and Computer Science Conference, ERK'96,
(Portoroz, Slovenia, September 1996), B:175-178. 1996.
back to index
