| Application domain: | Predicting mutagenesis |
| Further specification: | Data sets, html and LaTeX documentation |
| Pointers: | http://www.comlab.ox.ac.uk/oucl/groups/machlearn/mutagenesis.html |
| Data complexity: | 131 KB compressed file with positive and negative examples for the subsets of 188 and 44 compounds |
| Data format: | Progol |
| References: | (King et al. 1996), (Srinivasan et al. 1994) |
The prediction of mutagenesis is important as it is relevant to the understanding and prediction of carcinogenesis. Not all compounds can be empirically tested for mutagenesis, e.g. antibiotics. The considered dataset has been collected with the intention to search for a method for predicting the mutagenicity of aromatic and heteroaromatic nitro compounds. It comprises 230 compounds, divided into two sets of 188 (regression-friendly) and 42 (regression-unfriendly) compounds.
Of the molecules in the regression-friendly set, 125 have high mutagenic activity and 63 have low mutagenic activity.
Several levels of description of these molecules are available:
For STILL, positive examples are represented as definite
clauses:

We introduced another target predicate, named inactive,
the opposite of the active target concept. This allows the negative
examples to be also represented as definite clauses, the head of which
is built on the predicate inactive.
The experiments reported here consider the ![]() description of the molecules, and focus on the advantage of a Constraint
Logic Programming (CLP) formalism for induction. Many works have emphasized
how much the performance of symbolic learners depends on the way discretization
is performed. And the CLP formalism allows STILL to directly deal
with numbers with no need for a preliminary discretization. But
this could be only a slight advantage for the mutagenesis problem, as the
description of atoms contains very few distinct numerical constants;
this means that numerical constants could as well be handled as nominal
constants.
description of the molecules, and focus on the advantage of a Constraint
Logic Programming (CLP) formalism for induction. Many works have emphasized
how much the performance of symbolic learners depends on the way discretization
is performed. And the CLP formalism allows STILL to directly deal
with numbers with no need for a preliminary discretization. But
this could be only a slight advantage for the mutagenesis problem, as the
description of atoms contains very few distinct numerical constants;
this means that numerical constants could as well be handled as nominal
constants.
The advantage of CLP is checked by running STILL
with two different settings. In the first one, denoted by STILL![]() ,
only equality constraints are allowed (e.g. atom(X,Y,
Z,T), (Y=carbon),(Z=22),(T=.33)).
In the second one, denoted by STILL
,
only equality constraints are allowed (e.g. atom(X,Y,
Z,T), (Y=carbon),(Z=22),(T=.33)).
In the second one, denoted by STILL![]() ,
inequality constraints can be used as well ( atom(X,Y,Z,T),
(Y=carbon),(Z>20),(T<1.29)). The parameters
,
inequality constraints can be used as well ( atom(X,Y,Z,T),
(Y=carbon),(Z>20),(T<1.29)). The parameters ![]() and K were set to
and K were set to ![]() ,
K = 3.
,
K = 3.
The dataset was divided into a training set (90% of the 188 examples) and a test set (the remaining 10%), in such a way that the proportion of active/inactive molecules in the training set is roughly the same as in the whole dataset. The clauses learned from the training set were validated on the test set. An example remains unclassified if the test example admits no neighbour in the training set or if the majority vote ends up in a tie. The table below shows the percentage of correctly classified, misclassified and unclassified test examples, averaged on 15 independent selections of the training and test sets; the standard deviation on the percentage of correctly classified examples is also given. This procedure is very similar to a 10-fold cross validation; but results are averaged over 15 runs instead of 10, as suggested for stochastic processes.
The run time T (in seconds) on a HP-735 workstation, is
also given.
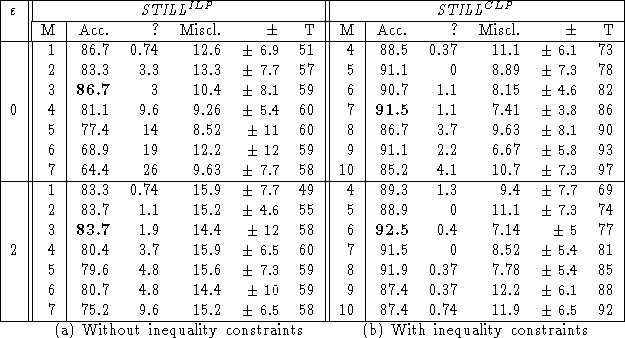
These results are (comparatively) quite good in what regards the predictive accuracy, and outstandingly good in what regards the computational cost.
Further, they show that induction effectively benefits from a CLP formalism on this dataset. Incidentally, the use of inequality constraints leads to more general hypotheses (an inequality is more often satisfied than an equality). This overgenerality is successfully overcome by increasing the parameter M, which controls the generality of hypotheses.
On the basis of these experiments, Constraint Logic Programming appears a valuable formalism in the sense it allows induction to effectively deal with both logic programming and numbers; in particular, it avoids the need for ad hoc numerical knowledge.
Besides, the heuristics adapted from DiVS and concerned
with tuning the degrees of consistency and generality of the clauses, through
parameters ![]() and M, appear to be quite efficient. Note that the tuning of
and M, appear to be quite efficient. Note that the tuning of ![]() and M takes place during classification, with no need to revise
the clauses learned. On going experiments are concerned with the automatic
adjustment of
and M takes place during classification, with no need to revise
the clauses learned. On going experiments are concerned with the automatic
adjustment of ![]() and M depending on the instance at hand.
and M depending on the instance at hand.
It learned rules that predict real number values for the the log mutagenicity. The linear equations express the class mostly in terms of Lumo or LogP. In comparison to Progol results (ten-fold cross validation) FORS yields marginally better accuracy (89% vs 88%).
For the regression friendly dataset, the additional attributes produced no significant improvement. The regression-unfriendly dataset of 42 molecules was transformed to a more regression-friendly one, yielding a correlation of 0.64 between the true and predicted log mutagenicity.