Predicting mutagenesis (OxUni+LAI+LRI)

Application domain:	Predicting mutagenesis
Further specification:	Data sets, html and LaTeX documentation
Pointers:	http://www.comlab.ox.ac.uk/oucl/groups/machlearn/mutagenesis.html
Data complexity:	131 KB compressed file with positive and negative examples for the subsets of 188 and 44 compounds
Data format:	Progol
References:	(King et al. 1996), (Srinivasan et al. 1994)

The data (OxUni)

The mutagenesis dataset originates from OxUni. Let us briefly recall the main features of this dataset.

The prediction of mutagenesis is important as it is relevant to the understanding and prediction of carcinogenesis. Not all compounds can be empirically tested for mutagenesis, e.g. antibiotics. The considered dataset has been collected with the intention to search for a method for predicting the mutagenicity of aromatic and heteroaromatic nitro compounds. It comprises 230 compounds, divided into two sets of 188 (regression-friendly) and 42 (regression-unfriendly) compounds.

Of the molecules in the regression-friendly set, 125 have high mutagenic activity and 63 have low mutagenic activity.

Several levels of description of these molecules are available:

• Background knowledge , composed of 10 137 facts, includes the description of all atoms and bonds in the 188 molecules. One molecule involves at most 40 atoms and 44 bonds.
• Background knowledge  stands for  augmented with numerical knowledge (e.g. the definition of the numerical predicate less-than).
• Background knowledge  stands for  augmented with two numerical attributes per molecule (i.e. the hydrophobicity of the molecule and the energy of the lowest unoccupied molecular orbital).
• Background knowledge  stands for  augmented with the definition of elementary structural chemical concepts (e.g. methyl or benzene groups).

Experiments with STILL (LRI)

This section describes the experiments performed in LRI with the stochastic learner STILL, on the mutagenesis problem.

For STILL, positive examples are represented as definite clauses:

We introduced another target predicate, named inactive, the opposite of the active target concept. This allows the negative examples to be also represented as definite clauses, the head of which is built on the predicate inactive.

The experiments reported here consider the  description of the molecules, and focus on the advantage of a Constraint Logic Programming (CLP) formalism for induction. Many works have emphasized how much the performance of symbolic learners depends on the way discretization is performed. And the CLP formalism allows STILL to directly deal with numbers with no need for a preliminary discretization. But this could be only a slight advantage for the mutagenesis problem, as the description of atoms contains very few distinct numerical constants; this means that numerical constants could as well be handled as nominal constants.

The advantage of CLP is checked by running STILL with two different settings. In the first one, denoted by STILL, only equality constraints are allowed (e.g. atom(X,Y, Z,T), (Y=carbon),(Z=22),(T=.33)). In the second one, denoted by STILL, inequality constraints can be used as well ( atom(X,Y,Z,T), (Y=carbon),(Z>20),(T<1.29)). The parameters  and K were set to , K = 3.

The dataset was divided into a training set (90% of the 188 examples) and a test set (the remaining 10%), in such a way that the proportion of active/inactive molecules in the training set is roughly the same as in the whole dataset. The clauses learned from the training set were validated on the test set. An example remains unclassified if the test example admits no neighbour in the training set or if the majority vote ends up in a tie. The table below shows the percentage of correctly classified, misclassified and unclassified test examples, averaged on 15 independent selections of the training and test sets; the standard deviation on the percentage of correctly classified examples is also given. This procedure is very similar to a 10-fold cross validation; but results are averaged over 15 runs instead of 10, as suggested for stochastic processes.

The run time T (in seconds) on a HP-735 workstation, is also given.
 

 
 

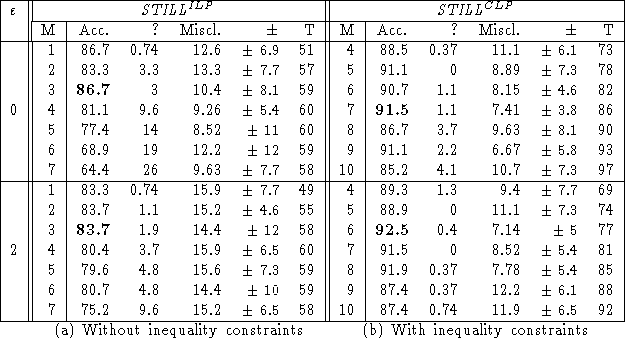
These results are (comparatively) quite good in what regards the predictive accuracy, and outstandingly good in what regards the computational cost.

Further, they show that induction effectively benefits from a CLP formalism on this dataset. Incidentally, the use of inequality constraints leads to more general hypotheses (an inequality is more often satisfied than an equality). This overgenerality is successfully overcome by increasing the parameter M, which controls the generality of hypotheses.

On the basis of these experiments, Constraint Logic Programming appears a valuable formalism in the sense it allows induction to effectively deal with both logic programming and numbers; in particular, it avoids the need for ad hoc numerical knowledge.

Besides, the heuristics adapted from DiVS and concerned with tuning the degrees of consistency and generality of the clauses, through parameters  and M, appear to be quite efficient. Note that the tuning of  and M takes place during classification, with no need to revise the clauses learned. On going experiments are concerned with the automatic adjustment of  and M depending on the instance at hand.

Experiments with FORS (LAI)

SAR problems are usually regression problems, reformulated to be classification problems for ILP purposes. The dependent (class) real-valued variable is the log mutagenicity (for ILP experiments, molecules that have positive log mutagenicity are considered mutagenic). FORS (First Order Regression System) was applied to the regression-friendly set of 188 examples with background knowledge  (Karalic and Bratko 1996).

It learned rules that predict real number values for the the log mutagenicity. The linear equations express the class mostly in terms of Lumo or LogP. In comparison to Progol results (ten-fold cross validation) FORS yields marginally better accuracy (89% vs 88%).

Experiments in regression with structural attributes (OxUni)

This dataset has been part of a set of experiments that examined the use of ILP-derived rules to aid the process of predicting the numerical activity of a molecule (Srinivasan and King 1996). In these experiments, structural concepts found by ILP were translated into boolean-valued attributes for multiple linear regression.

For the regression friendly dataset, the additional attributes produced no significant improvement. The regression-unfriendly dataset of 42 molecules was transformed to a more regression-friendly one, yielding a correlation of 0.64 between the true and predicted log mutagenicity.

References

1. A. Karalic, I. Bratko: First Order Regression. Machine Learning, Kluwer (in press).
2. R.D. King, S. Muggleton, A. Srinivasan, and M.J.E. Sternberg. Structure-activity relationships derived by machine learning: The use of atoms and their bond connectivities to predict mutagenicity by inductive logic programming. Proceedings of the National Academy of Sciences, 93:438-442, 1996.
3. M. Sebag, C. Rouveirol. Polynomial-time Learning in Logic Programming and Constraint Logic Programming. In S. Muggleton editor, Proceedings of the 6th International Workshop on Inductive Logic Programming, 1996.
4. A. Srinivasan, S. Muggleton, R.D. King, and M.J.E. Sternberg. Mutagenesis: ILP experiments in a non-determinate biological domain. In S. Wrobel, editor, Proceedings of the 4th International Workshop on Inductive Logic Programming, volume 237 of GMD-Studien, pages 217-232. Gesellschaft für Mathematik und Datenverarbeitung MBH, 1994.
5. A. Srinivasan and R.D. King. Feature construction with inductive logic programming: A study of quantitative predictions of biological activity aided by structural attributes. In S. Muggleton, editor, Proceedings of the 6th International Workshop on Inductive Logic Programming, pages 352-367. Stockholm University, Royal Institute of Technology, 1996.

back to index