Early diagnosis of rheumatic diseases (LAI)

Correct diagnosis in the early stage of rheumatic disease is a difficult problem. Having passed all the investigations, many patients can not be reliably diagnosed after their first visit to the specialist. The reason is that anamnestic, clinical, laboratory and radiological data of patients with different rheumatic diseases are frequently similar.
Application domain: Early diagnosis of rheumatic diseases
Further specification: Data set
Pointers: Contact Nada Lavrac Nada.Lavrac@ijs.si
Data complexity: 426 examples, 16 attributes
Data format: Prolog

The data

Data about 462 patients were collected at the University Medical Center in Ljubljana (Pirnat et al. 1989). There are over 200 different rheumatic diseases which can be grouped into three, six, eight or twelve diagnostic classes. Eight diagnostic classes were considered, as in the experiments of Karalic and Pirnat (1990).

To facilitate the comparison with earlier experiments in rule induction in this domain (Lavrac et al. 1993), the experiments were performed on anamnestic data, without taking into account data about patients' clinical manifestations, laboratory and radiological findings. The sixteen anamnestic attributes are as follows: sex, age, family anamnesis, duration of present symptoms (in weeks), duration of rheumatic diseases (in weeks), joint pain (arthrotic, arthritic), number of painful joints, number of swollen joints, spinal pain (spondylotic, spondylitic), other pain (headache, pain in muscles, thorax, abdomen, heels), duration of morning stiffness (in hours), skin manifestations, mucosal manifestations, eye manifestations, other manifestations and therapy.

A specialist for rheumatic diseases has provided his knowledge about the typical co-occurrences of symptoms. Six typical groupings of symptoms were suggested by the specialist as background knowledge to be considered by the learner (Lavrac et al. 1993).

The first grouping relates the attribute ``Joint pain'' and the attribute ``Duration of morning stiffness''.

The second grouping relates the spinal pain and the duration of morning stiffness. The third grouping relates the attributes sex and other pain. The fourth grouping relates joint pain and spinal pain. All co-occurrences are characteristic. The fifth grouping relates joint pain, spinal pain and the number of painful joints. The last, sixth, grouping relates the number of swollen joints and the number of painful joints.

The background knowledge is encoded in the form of functions, introducing specific function values for each characteristic combination of symptoms. All the other combinations (except the ones explicitly specified above) have the same function value irrelevant.

LINUS with CN2 and kNN experiments

We applied LINUS to generate additional attributes from the background knowledge, then used the kNN instance-based learning algorithm on the resulting problem. kNN with and without feature weights was used. For comparison, we also evaluated the performance of CN2 with the Laplace and the m-estimate. Experiments without background knowledge were also conducted (Dzeroski and Lavrac 1996). Ten different partitions of the data set into 70% training and 30% testing examples were used.

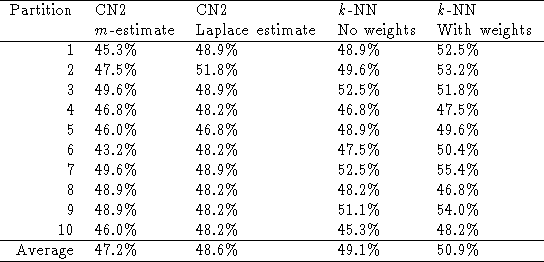
The classification accuracies of CN2 and of k-NN are given in the table below. Background knowledge improves the performance in all cases. For CN2 with the m-estimate, CN2 with the Laplace estimate, k-NN without feature weights and k-NN with feature weights, respectively, the differences are significant at the 90%, 98%, 88%, and 83% levels.
 

tabular208

In terms of accuracy, CN2 with the Laplace estimate performs better than CN2 with the m-estimate. However, it performs worse in terms of relative information score (Dzeroski and Lavrac 1996). k-NN with feature weights performs better than CN2. The difference is significant at the 99.5% level for CN2 with the m-estimate and at the 98% for CN2 with the Laplace estimate. k-NN without feature weights also performs slightly better than CN2.

The best value of m for the ten partitions was 16 in four cases, 32 in three cases, and 64 in three cases. In nine of the ten cases, the best value of m was lower when background knowledge was given, i.e., the dataset appears to contain less noise when background knowledge is given. A similar effect can be noticed for the parameter k: it ranged from 7 to 21 with an average of 13 and was lower in the presence of background knowledge for eight of the ten partitions. This indicates that background knowledge alleviates the effects od data imperfections in this domain.

References

  1. S. Dzeroski, N. Lavrac. Rule induction and instance-based learning applied in medical diagnosis. Technology and Health Care, 4, 203-221. Elsevier, 1996.
  2. Karalic, A., and Pirnat, V. (1990). Machine learning in rheumatology. Sistemica 1(2): 113-123.
  3. Lavrac, N., Dzeroski, S., Pirnat, V., and Krizman, V. (1993). The utility of background knowledge in learning medical diagnostic rules. Applied Artificial Intelligence, 7:273-293.
  4. Pirnat, V., Kononenko, I., Janc, T., and Bratko, I. (1989). Medical analysis of automatically induced rules. In Proc. 2nd European Conference on Artificial Intelligence in Medicine, pages 24-36. Springer, Berlin.

back to index